Note
Go to the end to download the full example code
Boolean Operations#
Perform boolean operations with closed (manifold) surfaces.
Boolean/topological operations (intersect, union, difference) methods
are implemented for pyvista.PolyData mesh types only and are
accessible directly from any pyvista.PolyData mesh. Check out
pyvista.PolyDataFilters and take a look at the following
filters:
Essentially, boolean union, difference, and intersection are all the same operation. Just different parts of the objects are kept at the end.
The - operator can be used between any two pyvista.PolyData
meshes in PyVista to cut the first mesh by the second. These meshes
must be all triangle meshes, which you can check with
pyvista.PolyData.is_all_triangles.
Note
For merging, the + operator can be used between any two meshes
in PyVista which simply calls the .merge() filter to combine
any two meshes. This is different from boolean_union as it
simply superimposes the two meshes without performing additional
calculations on the result.
Warning
If your boolean operations don’t react the way you think they
should (i.e. the wrong parts disappear), one of your meshes
probably has its normals pointing inward. Use
pyvista.PolyDataFilters.plot_normals() to visualize the normals.
import pyvista as pv
sphere_a = pv.Sphere()
sphere_b = pv.Sphere(center=(0.5, 0, 0))
Boolean Union#
Perform a boolean union of A and B using the
pyvista.PolyDataFilters.boolean_union() filter.
The union of two manifold meshes A and B is the mesh
which is in A, in B, or in both A and B.
Order of operands does not matter for boolean union (the operation is commutative).
result = sphere_a.boolean_union(sphere_b)
pl = pv.Plotter()
_ = pl.add_mesh(sphere_a, color='r', style='wireframe', line_width=3)
_ = pl.add_mesh(sphere_b, color='b', style='wireframe', line_width=3)
_ = pl.add_mesh(result, color='lightblue')
pl.camera_position = 'xz'
pl.show()

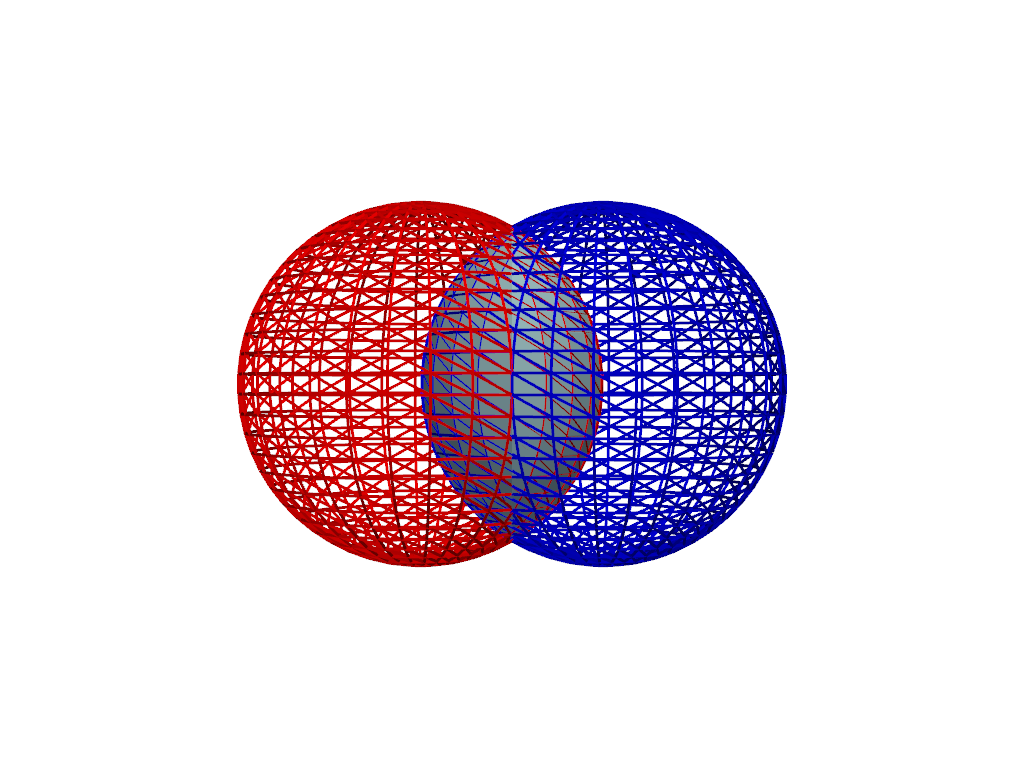
Boolean Difference#
Perform a boolean difference of A and B using the
pyvista.PolyDataFilters.boolean_difference() filter or the
- operator since both meshes are pyvista.PolyData.
The difference of two manifold meshes A and B is the volume
of the mesh in A not belonging to B.
Order of operands matters for boolean difference.
result = sphere_a.boolean_difference(sphere_b)
pl = pv.Plotter()
_ = pl.add_mesh(sphere_a, color='r', style='wireframe', line_width=3)
_ = pl.add_mesh(sphere_b, color='b', style='wireframe', line_width=3)
_ = pl.add_mesh(result, color='lightblue')
pl.camera_position = 'xz'
pl.show()
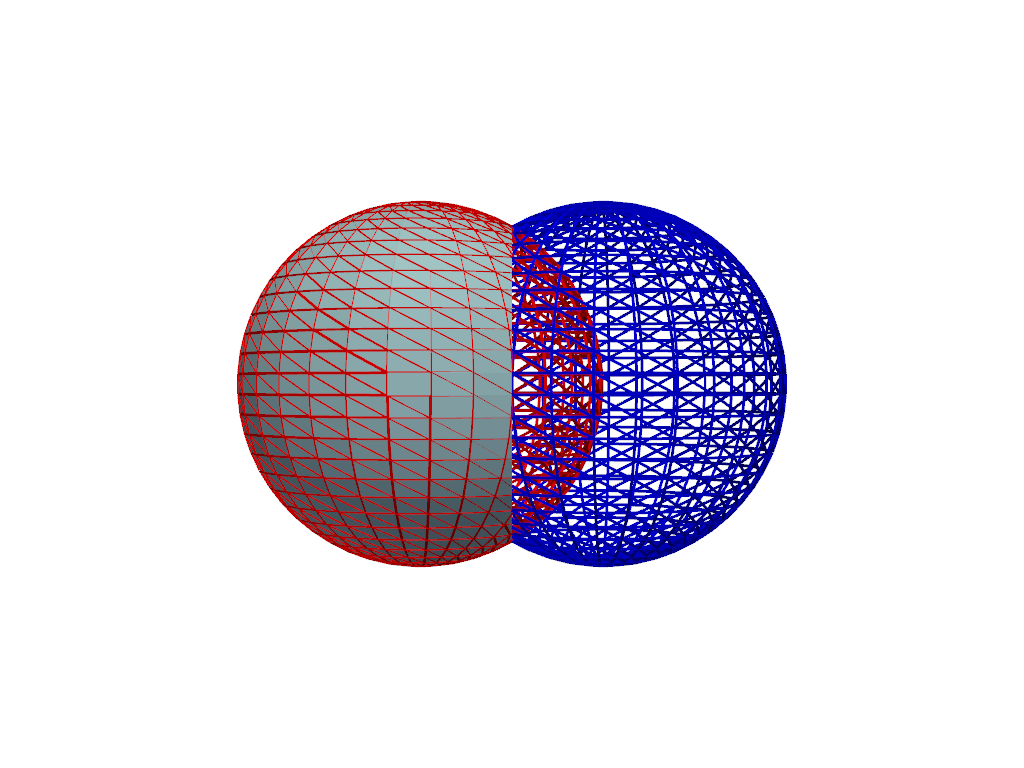
Boolean Intersection#
Perform a boolean intersection of A and B using the
pyvista.PolyDataFilters.boolean_intersection() filter.
The intersection of two manifold meshes A and B is the mesh
which is the volume of A that is also in B.
Order of operands does not matter for boolean intersection (the operation is commutative).
result = sphere_a.boolean_intersection(sphere_b)
pl = pv.Plotter()
_ = pl.add_mesh(sphere_a, color='r', style='wireframe', line_width=3)
_ = pl.add_mesh(sphere_b, color='b', style='wireframe', line_width=3)
_ = pl.add_mesh(result, color='lightblue')
pl.camera_position = 'xz'
pl.show()
Behavior due to flipped normals#
Note that these boolean filters behave differently depending on the orientation of the normals.
Boolean difference with both cube and sphere normals pointed outward. This is the “normal” behavior.
cube = pv.Cube().triangulate().subdivide(3)
sphere = pv.Sphere(radius=0.6)
result = cube.boolean_difference(sphere)
result.plot(color='lightblue')

Boolean difference with cube normals outward, sphere inward.
cube = pv.Cube().triangulate().subdivide(3)
sphere = pv.Sphere(radius=0.6)
sphere.flip_normals()
result = cube.boolean_difference(sphere)
result.plot(color='lightblue')

Boolean difference with cube normals inward, sphere outward.
cube = pv.Cube().triangulate().subdivide(3)
cube.flip_normals()
sphere = pv.Sphere(radius=0.6)
result = cube.boolean_difference(sphere)
result.plot(color='lightblue')

Both cube and sphere normals inward.
cube = pv.Cube().triangulate().subdivide(3)
cube.flip_normals()
sphere = pv.Sphere(radius=0.6)
sphere.flip_normals()
result = cube.boolean_difference(sphere)
result.plot(color='lightblue')

Total running time of the script: (0 minutes 5.838 seconds)